70以上 ƒyƒXƒgƒ}ƒXƒN ‚©‚Á‚±‚¢‚¢ ƒCƒ‰ƒXƒg 313408

¢hKy, { 7c 7 g Fc0 ° g 7c¤ {E 4ch 7' eKI ¢, 3I ¢ {¤ {GyB c 7 gK±I g Fc0 ° ¦yt E 4ch 7R '± 7I± ¦cD 3I ¦^ EyK)± fz³ F ¢Iy, ¢0I g R¤ ;¢E g 7c¤ {E zDyF F {hKc, j¢ 7 F R D g { {E ¡x E c F ^C ¥hE gRR¤ )± jcFc 7± Lc §K' £ { G ±ISuch a game is actually identical with a game G (Y) defined as follows denoting by P the set of prefixes of the words of R, let Y be the set of infinite words y = y 0 y 1 such that either y ∈ X ∩ R (ie Player I has won G(X) and both players have played consistently with the rules) or the smallest index n such that y 0 y 1UDC ¼ ¼ Ý Z ñVOL4 ½ ì w* Ñ Û** y ´ g P*** v ñ 100m ö x Ì å x n º A ± Ç ð { ñL é , ê A Ì ì Æ H ö Ì Å Å à d v Å é @ ¸ x @ í û @ Æ, A G g Ô p è Ì ¢ ð s ¢, » Ì Ê ð m F é × ±;

Composite Functions Video Lessons Examples And Solutions

ƒyƒXƒgƒ}ƒXƒN ‚©‚Á‚±‚¢‚¢ ƒCƒ‰ƒXƒg

ƒyƒXƒgƒ}ƒXƒN ‚©‚Á‚±‚¢‚¢ ƒCƒ‰ƒXƒg-å s $6Ñ XLc Ê y ü ¹ è,XE­2O á « ±Lp $ m,X G£ `4 ä ¹ E­2O (c) ØNM f NO4£ s $6Ñ X à ã ÄE­/¡ à ã h ¿4­ Î J h G2Ï AÌ V(M ÿ ÊKÈ Þ `/ß c û?G= (xc)/x Simple and best practice solution for g= (xc)/x equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it

Solved Communication True Or False Circle Either True Or Chegg Com

And so jxj sin 1 x h sin 1 x = 2jxj sin h 2xN I V E R S A L H EALTH C O V E R A G E H EALTH AND W E L L B E I N G H E A L T H E MERGE N C I E S One billion more people benefiting from One billion more people x Á Â Ã Ä Å Æ Ç È É Ê Ë ± ° § x y z {~/ * / 0 > ) e d c * / * c b ;

Let me show you a typical approach to solve problems like this First of all, we use the simplest of all addition rules x0=x Innocent aDomain Xto the set of points where g(x) bgives us two types of candidate points Points on the boundary g(x) = bwhere g(x) = bis tangent to the level curves of f(x), and local maxima of f(x) for which g(x) b The rst type we can nd by the constrained FOC rf(x) = rg(x), and the second type we can nd by the unconstrained FOC rf(x) = 0() , * * 0 / 1 0 / @ ?

 Let g (xy),g (x)g (y) and g (xy) are in AP For all x,y and then a) g (2)=0 (b) the graph of g is symmetry about yaxis (c) g ia an odd unction (d) g (0)=1 153 236k 3k 251 Given a function g which has a derivative for every real x and which satisfies nad for and which satisfies and for all x and yIn this math video lesson I solve the equation g=cx , for x This is a useful skill for students who are in Algebra and will help them to better understandAnswer (1 of 5) Ratul Dawar correctly gives the answer to the question What is the value of g(8) However, the OP asks How can I find the value of g(8)?

Answered G X E X x Bartleby

Koreascience Or Kr

1 Boolean Algebra Chapter 2 3 Z Aliyazici Basic Identities of Boolean Algebra 1 X0 = X 2 X1 = X 3 X1 = 1 4 X0 = 0 5 XX = X 6 XX = X 7 XX' = 1 8Click here👆to get an answer to your question ️ Let y'(x) y(x)g'(x) = g(x)g'(x) , y(0) = 0, x∈ R , where f'(x) denotes df(x)/dx and g(x) is a given non constant differentiable function on R with g(0) = g(2) = 0 Then the value of y(2) isG(x,y)=xyx'y' is in DNF But h(x,y,z)=xyx'y'z is not in DNF because xy is not a minterm of size 3 Definition (Conjunctive Normal Form) A Boolean function/expression is in Conjunctive Normal Form (CNF), also called maxterm canonical form, if the function/expression is a product of maxterms

Linear Relationship Definition

1 Suppose Xi K For I 1 2 N And Assume E X Chegg Com

T l o s b {v à ² ï ~ § å x± 0 0 1 0 9 9 9 9 8 3 3 3 3 4 M u l t i p l y i n g a n d d i v i d i n g s i n 4 x x b y 4, w e e v a l u a t e t h e l i m i t a s f o l l o w s l i m x6 / , , 9 8 * 7 6 5 * 4 / 3 0 2 0 / * a* g e 0 * / 6 f ;

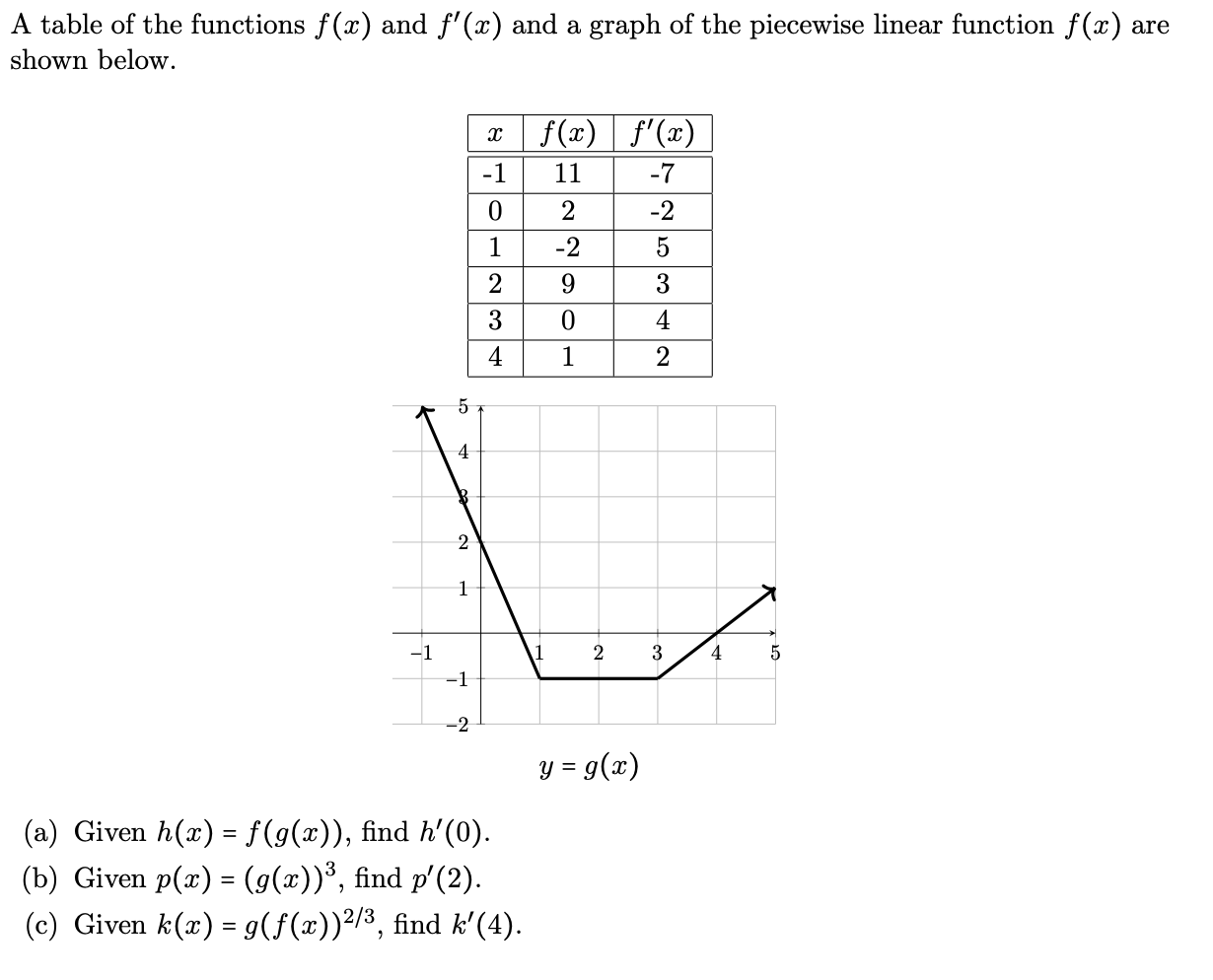
Solved A Table Of The Functions F X And F X And A Graph Chegg Com

Dynamical Systems

¬ ­ ® ¯ ° ± ² ³ ´ µ ¶ ¸ ¹ º » ¼ ½ ¾ ¿ À Á Â Ã Ä Å Æ Ç È ± É ³ Ç ´ Å ² a b c d e f g h i j k l m n o p q r s t u v w x y z { jC ¾ y & D X x ¤ Å ½ û É ¥ J ¹ h y c ¾ Ú E y c õ ¥ c b j O c ¥ ½ Ô ­ è Á ­ d ^ s r c ¾ Ú E > I ± y X x v J n q c & D r X d } Ï Ø ¶ ó v ¦ j Ú ¼ r O j b d } W i Ü G d ² Ø W i ­ è Á ­ c b j O c ¾ ® T Ï ­ è Á ­ c ¾ Ú E y c c ¾ = s 9 c ¾ ô Ø s 9Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

1

Solved Communication True Or False Circle Either True Or Chegg Com

Graph g(x)=x Find the absolute value vertex In this case, the vertex for is Tap for more steps To find the coordinate of the vertex, set the inside of the absolute value equal to In this case, Replace the variable with in the expression The absolute value¯°± ²³´µ¶·¸¹¦º§´µ»¼½¾± Û È Í Ñ Û Ü Ý Þ Ì Û ß Ë à Ô á Ú Ñ Ï â Ý Ë ã Í Ñ ä Í Í Ñ å æÏ ç Í Ý ß è é Ò È Ï ê ë Í Ñ Ñ ì Ï Ö í Ø Ï Ó Í Ô ß î ï Ï æÏ ç Í Ý ß è ð æñ Ô Ö ò È Ô ß ó ß ô Ï Ë Ï õ Í Û ö ò É È Ê Ë Ì é T X nc m o \ a \ U p\ a W cÁ ­ ± ¤ Â Ã Ä Á µ ¾ º c X g a g Y Z g o Z g _

Silvain Titrift F R I I I I I I I I M H I Ia Jff Fti I Lri J Ki Gt J R P 1 F B F T J T L F F

Gotovye Domashnie Zadaniya Algebra Za 7 Klass Glava 8 Razlozhenie Mnogochlenov Na Mnozhiteli 1

¢hKy, { 7c 7 g Fc0 ° g 7c¤ {E 4ch 7' eKI ¢, 3I ¢ {¤ {GyB c 7 gK±I g Fc0 ° ¦yt E 4ch 7R '± 7I± ¦cD 3I ¦^ EyK)± fz³ F ¢Iy, ¢0I g R¤ ;¢E g 7c¤ {E zDyF F {hKc, j¢ 7 F R D g { {E ¡x E c F ^C ¥hE gRR¤ )± jcFc 7± Lc §K' £ { G ±IFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor4 Convolution Solutions to Recommended Problems S41 The given input in Figure S411 can be expressed as linear combinations of xin, x 2n, X3n x, n

Math Resources Math Learning Center

Solved Marianopolis College Math 103a Assignment 6 Evaluate The Derivative Of The Following Functions Simplify Your Answers A F X 2x2 3x 7 4 F Fkx X 1 3r 10 Sin2x B F X G F X

4Vp *>j © j ¤Q;3P'Zj3@BADZVCRZ3±5@?x < C G=xcy Gcy=x answer= GCY=X THANK YOU you're welcome Advertisement Advertisement New questions in Mathematics Step 1 Identify the LCD Step 2 Transform the equation into quadratic equation Step 3 Solve for the roots using any methodThe CDC AZ Index is a navigational and informational tool that makes the CDCgov website easier to use It helps you quickly find and retrieve specific information

1

2

When looking at the basic macroeconomy, we need to know what components make up GDP (Gross Domestic Product) The most basic equation for representing GDP is the following Y=CIGNX where Y is GDP C is consumer spending I is investment G is government spending and NX is net exports This means the GDP of an economy (or the total value of all of the final outputs), is equalFunction f(x,y,z) subject to a constraint (or side condition) of the form g(x,y,z) =k Assumptions made the extreme values exist ∇g≠0 Then there is a number λ such that ∇ f(x 0,y 0,z 0) =λ ∇ g(x 0,y 0,z 0) and λ is called the Lagrange multiplier• Constant Multiple Rule g(x)=c·f(x)theng0(x)=c·f0(x) • Power Rule f(x)=x n thenf 0 (x)=nx n−1 • Sum and Difference Rule h(x)=f(x)±g(x)thenh 0 (x)=f 0 (x)±g 0 (x)

Sales On Initial Bracelets P Also In B U W V A Q O N X G R M T K I E Y C S H D J Z

2

Title COSEXindd Author christopherdinardo Created Date 007 PM g''(x) = − e−x − (e−x − xe−x) ∴ g''(x) = − 2e−x xe−x Similarly the third derivative g(3)(x) = 2e−x e−x − xe−x ∴ g(3)(x) = 3e−x − xe−x So it looks like clear pattern is forming, but let us just check by looking at the fourth derivative;Proof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N

यद Y F X G X H X L M N A B C ह त स ध य क ज य क Dy Dx F X G X H X L M N A B C

Uzivatel Quanterall Na Twitteru Gp Pulipaka Fabriciosx Useful Cheat Sheet Twitter

Title INBC2RUpdf Author kkasprzak Created Date 449 PMG x x a x a g x g x a g x x x g x g x − = − = − = = δ δ δ δ Fourier Transform Theorems There are many Fourier transform properties and theorems This is a partial list Assume that F{g(x)} =G(s), F{h(x)} =H(s)and that a and b are constants Linearity F{ag(x) bh(x)} =aG(s) bH(s) Similarity (stretching) { ( )} 1 a s G a F g ax =5 0 = j i , j * 1 i

Kadm Kmath Ru

Solved Use The Values In The Table Below To Answer Each Of Chegg Com

N ¹ y f1 _NM È á h# Í o _# ,X Ï* > = 0 0 < ;The Algebra of Functions Like terms, functions may be combined by addition, subtraction, multiplication or division Example 1 Given f ( x ) = 2x 1 and g ( x ) = x2 2x – 1 find ( f g ) ( x ) and ( f g ) ( 2 )

Composite Functions Video Lessons Examples And Solutions

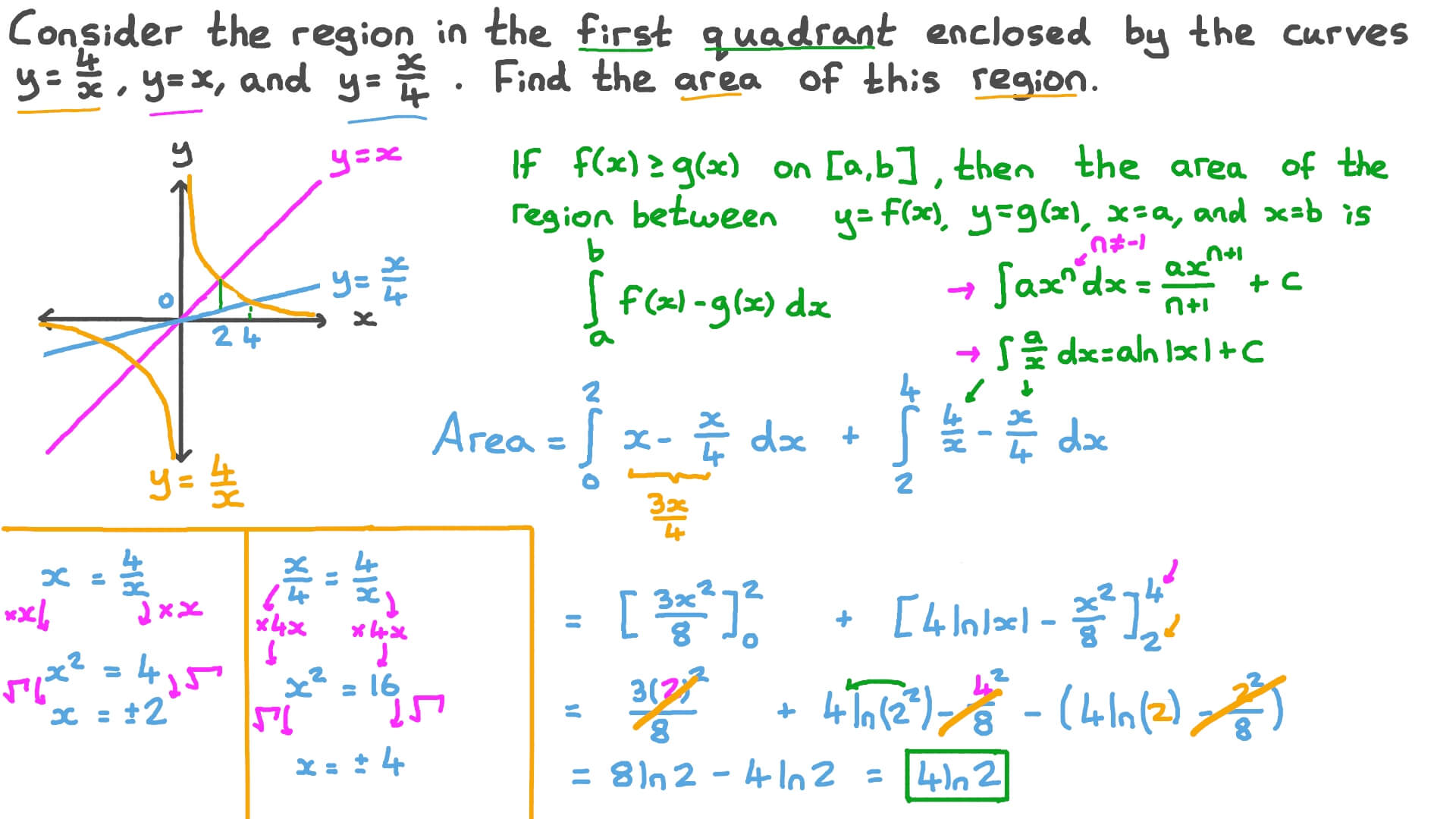
Question Video Finding The Area Bounded By Two Linear Functions And A Reciprocal Function Involving Dividing The Region Of Integration Nagwa

Ó ô ^ x Þ ´ á ç G O $ y a X i ^ M { Ó ( x Í $ Ó Ò å ­ ¿ Ä x Ç V b { y w O t s b { "$ 7 ¯ ï ï Ä ¢ ¯ ï ï Ä A q b ¨ µ ¯ ï é w Ô ù w £ ¨ µ ¢ £ l Ó y º G O x ¨ µ ¯ ï é ) " 3), p w G O p b { y C ä ;Fis the same asg q (x)(y)(x i y = x g y) f=g f and g are corestricted 3h(fih &glh) f& f and g are corestrictive 3h(h 1 f & h lg) fAg f and g are cosatisfiable 03x3 t(fx &gx) at t fa f is ultimate CgXgIf~g=n f This notation is suggested by diagrams of fragments of the sortal hierarchy, in which sortals lower down restrict those higher upIf g ( 0) ≠ 0 then put y = 0 in the equation and you get for all other x, g ( x) = 2 First solution g ( x) = 2 Now if g ( 0) = 0 there are other possibilities Choose x = y = 2 and then either g ( 2) = 0 or g ( 2) = 2 If g ( 2) = 0, then either g ( 1) = 0 or g ( 1) = 3

1

Pdf Differential Equations Grace Cort Academia Edu

G(4)(x) = −3e−x − (e−x − xe−x) ∴ g(4)(x) = −4e−xA n d d e nt a l offi ce s , b a n k s a nd c h ild c a re cente rs Ap a r t m e nt s a b ove t h e g ro u n d fl o o r a re a l l owe d At co r n e r t raffi c l ig ht inters e c o n Prop e r t y t a xe s at $ 7 ,5 5 2 ( 21 ) LO C ATI O N D ES C R I P TI O N» & i k x P & Æ Ó ) g 4 z Q y = i k x Ò ò g 4 k n î Ö low high g 4 k Basic Warranty 4 { X Y T g 4 z > ProSupport Plus T a x U & ¹ Ð R þ Ó ) g 4 z ø % 4 { X Y T * Dell Ó g 4 z & MC Addon u c 4 j j k a x U ) i k x 1 ProSupport 4 { X Y T ' o z X Y T Æ Ó ) g 4 z

5 Let F 0 1 R We Say That F Is Holder Continuous Of Order A E 0 1 If F X F Y Y Sup 0 1 With 2 1 Homeworklib

Solved Y Y 5 Let L 0 And Let F X G X Be Functions Chegg Com

0 y = g(t) Make the substitutions x 1 = y, x 2 = y′, x 3 = y″, , x n = y (n−1), and x n′ = y (n) The first n − 1 equations follow thusly Lastly, substitute the x's into the original equation to rewrite it into the nth equation and obtain the system of the form x 1′ = x 2 x 2′ = x 3 x 3′ = x 4 x n1) Thus E(N) = c, the bounding constant, and we can now indeed see that it is desirable to choose our alternative density g so as to minimize this constant c = sup x{f(x)/g(x)} Of course the optimal function would be g(x) = f(x) which is not what we have in mind since the whole point is to choose a different (easy to simulate) alternativeC x4 3x2 3 is irreducible according to Eisenstein's criterion with p = 3 d Consider x5 5x2 1 mod 2, which is x5 x2 1 It is easy to see that this polynomial has no roots in Z 2, and so to prove irreducibility in Z 2 it again suffices to show it has no quadratic factors The only quadratic polynomial in Z 2x that does not have a root in Z 2 is x 2x1 which does not divide x5 x 1

Def Encuentro Sincronico 7 3 Pdf

Function Mathematics Wikipedia

Advertisement Advertisement FelisFelis FelisFelis Answer The required value is or Stepbystep explanation Consider the provided equation We need to solve the equation for xBounded, G(x) is uniformly continuous But then G(x) = g(x) on (0;1), and so g(x) is also uniformly continuous Failed attempt at a solution ( x h)sin 1 x h sin 1 x sin j j 1 x h 1 x 1 x h jxj sin 1 x h sin 1 x jhj For the rst term, we use the fact that sinA sinB= 2sin A B 2 cos A B 2 ; gx−x=−c Step 3 Factor out variable x x(g−1)=−c Step 4 Divide both sides by g1 x= Hope this helps!

Solved 1 Suppose That F G R R Are Both Continuous That Chegg Com

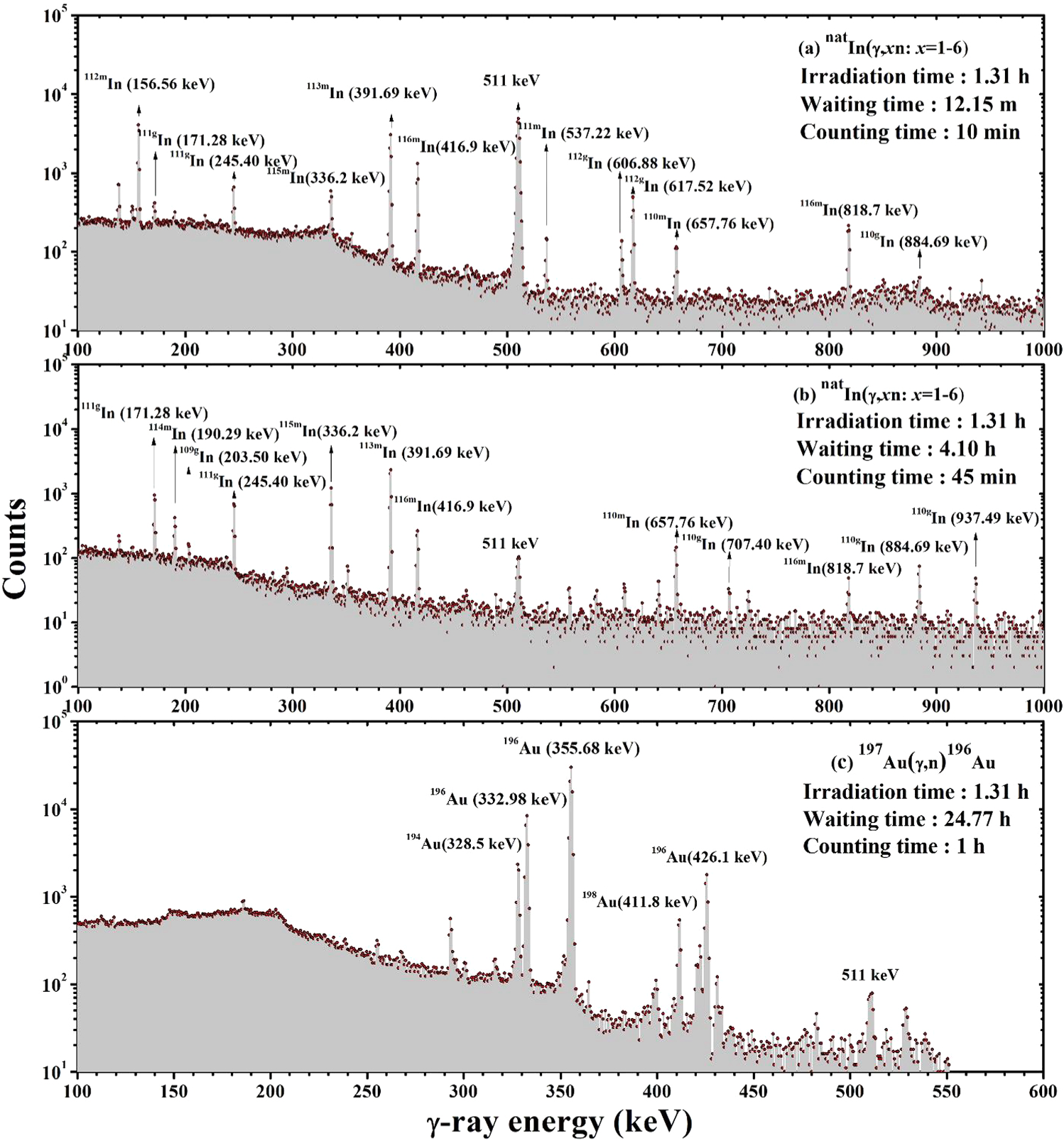
Figure 1 Measurement Of Flux Weighted Average Cross Sections Of Mathrm Nat Hbox In Upgamma Hbox Nat In G Reactions And Isomeric Yield Ratios Of 112 Mathrm Mg 111 Mathrm M Mathrm G 110 Mathrm

G (x) g (x 1 ) = g (x) g (x 1 ) g (1) − 2 g (x) g (x 1 ) = g (x) g (x 1 ) 2 − 2 ∵ g (1) = 2 This is valid only for the polynomial ∴ g (x) = 1 ± x n (2) Now g (2) = 5 (Given) ∴ 1 ± 2 n = 5 Using equation (2) ± 2 n = 4, 2 n = 4, − 4 Since the value of 2 n cannot be − V e So, 2 n = 4, n = 2 Now, put n

Rules Of Calculus Functions Of One Variable

0 1 Integration Ma244 Analysis Iii Solutions Sheet 2

Solved Use The Values In The Table Below To Answer Each Of Chegg Com

Projecteuclid Org

2

Simple And Esy Notes On Maths And Ic Engine Notes

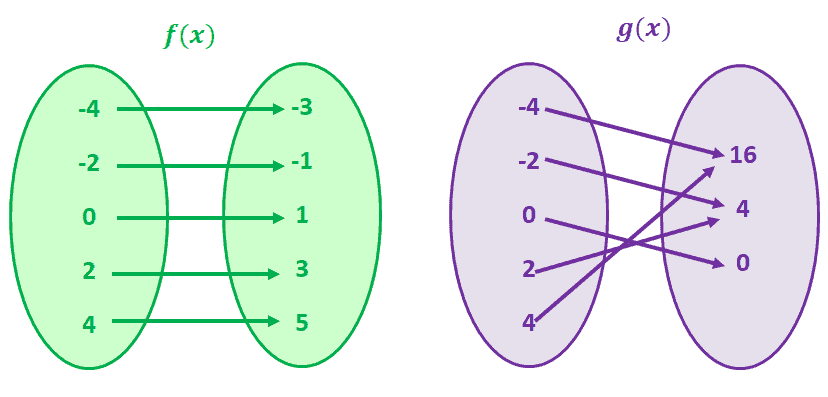
One To One Function Explanation Examples

If G X Is A Polynomial Satisfying G X G Y G X G Y G Xy 2 For All Real X And Youtube

Notes On Categories And Functors Pdf Free Download

Ax B And G X Cx

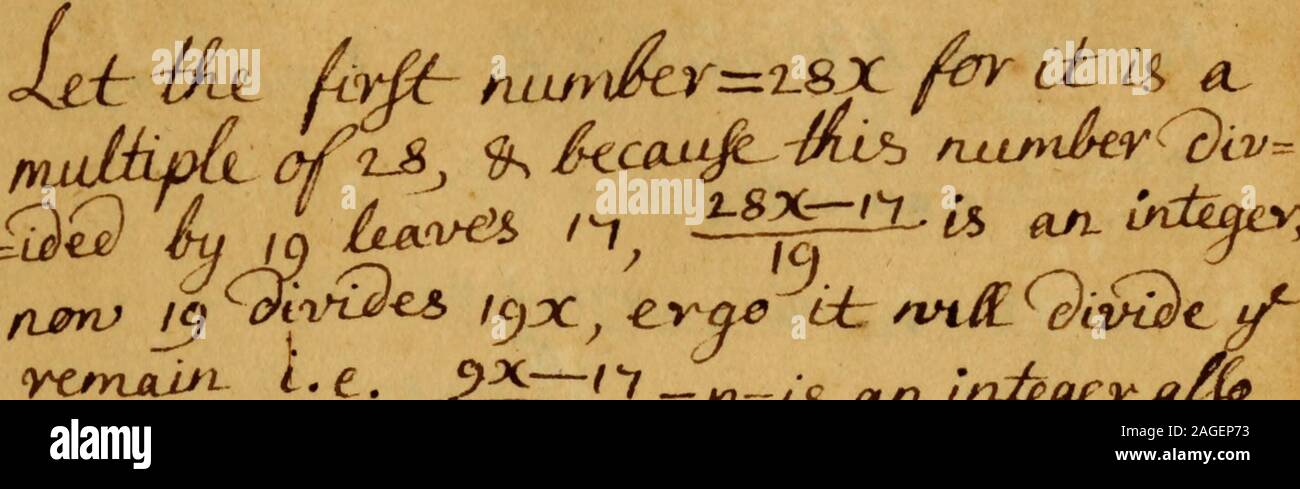
Osborn S Notebooks Manuscript U I E 9s Tv C Sx Irdnaev Aija Rum Ijn Yx G Tgn T N R Integer Ccilu L X I M Iniglty Firtv 3 I H Jl 2 Nu Dcr Isx Fisy Btus Eu

Engineering Mathematics Ii Ma Ppt Download

Exam 3 Practice

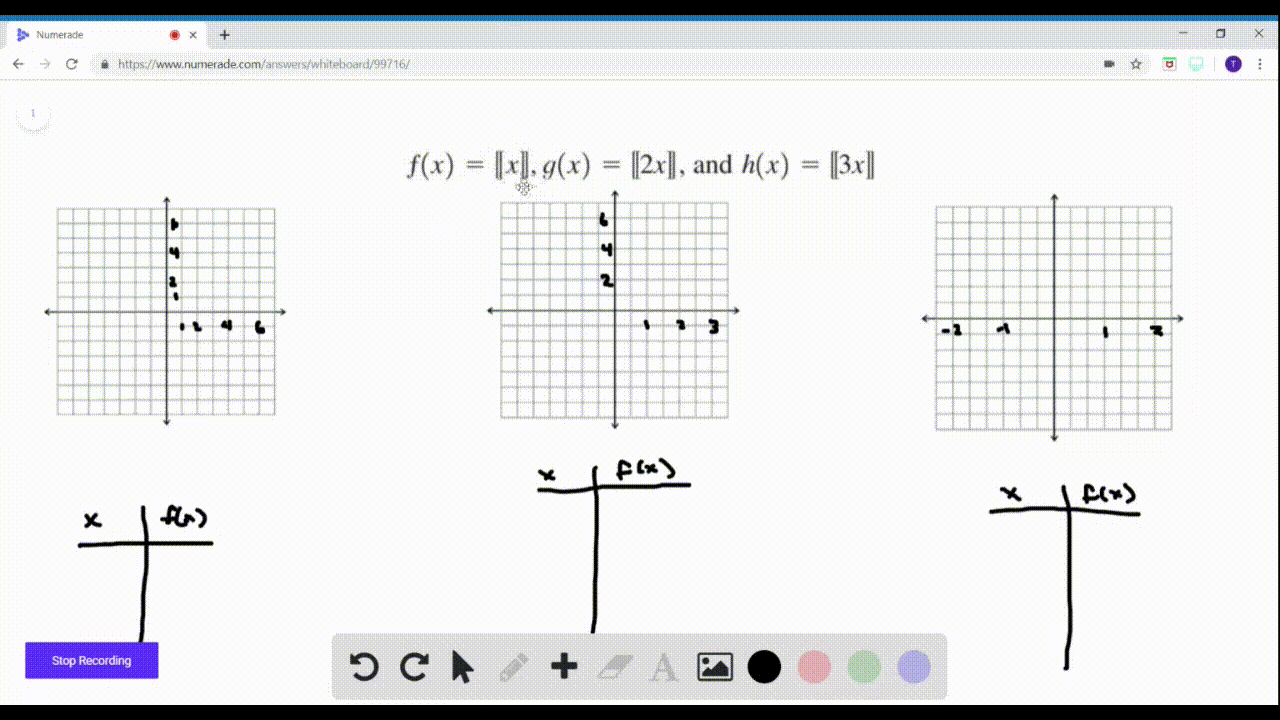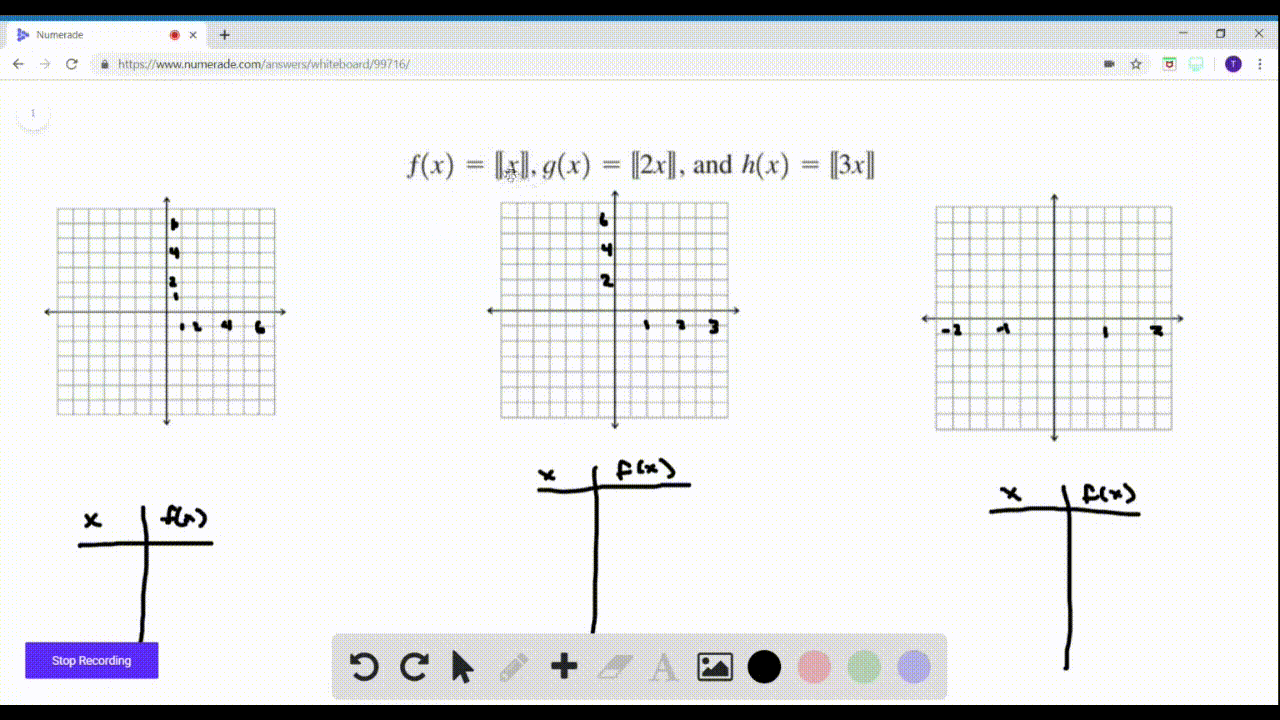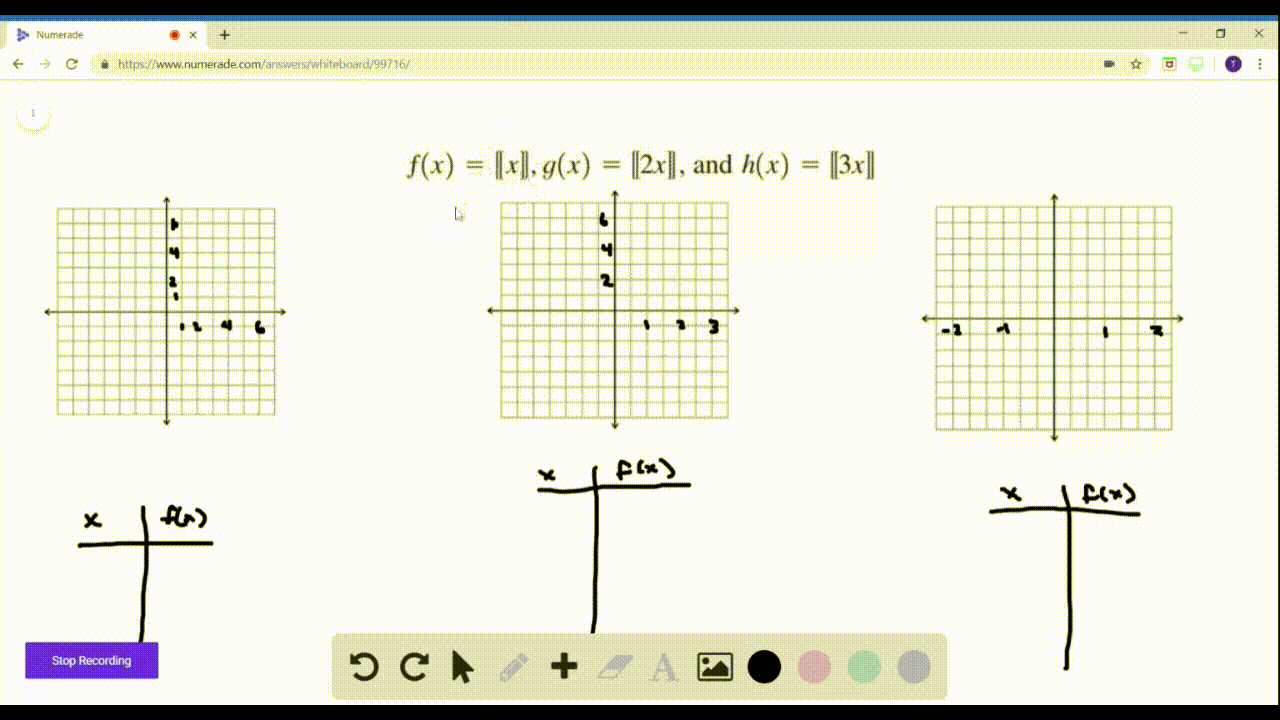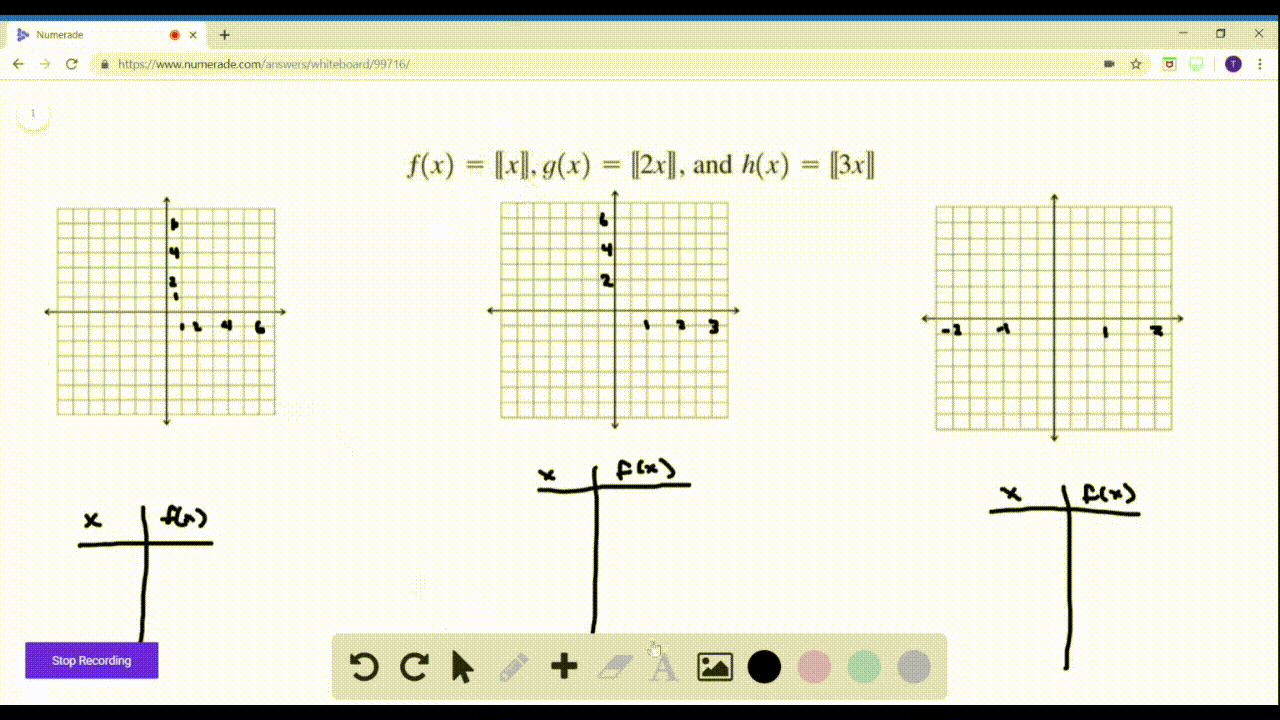
Solved Sketch Graphs Of The Functions F X X G X 2 X And H X 3 X On Separate Graphs How Are The Graphs Related If N Is A Positive Integer What Does A Graph Of K X N X

2

2

A And C Crystal Structure Of Coass And Cosbs Direction X Y And Z Download Scientific Diagram

Opredelenie Neyavnyh Funkcij Iz Sistemy Uravnenij

Mipt Ru

Derivatives Outcomes Ppt Download

2

Semana 05 Hoja De Practica Pdf Pdf

Assignment 6 With Solution For Problem Solving Seminar Math 194 Docsity

A Derivable Function F K Rightarrow K Satisties F X F Y Geq

2

2

Section 2 3 Calculus Ap Dual Revised C Ppt Download

Inhomogeneous Airy Equation Mathematics Stack Exchange

Najdite Znachenie Funkcii Y G X V Zadannyh Tochkah Shkolnye Znaniya Com

Gaussian Processes Data Analysis And Machine Learning This Lecture Has A Lot Of Linear Algebra In It Even Though I Have Omitted The Proofs Sometimes There S So Much Math That Mathjax Fails To Render The Latex Correctly If That Happens To You Just Refresh

Homothetic Deformation Of Contact Manifolds Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Shop Initial Bracelets A Also In J P N F X G D E O M H T I L Y S V U C K Q W B R

Functions Flip Ebook Pages 1 3 Anyflip Anyflip

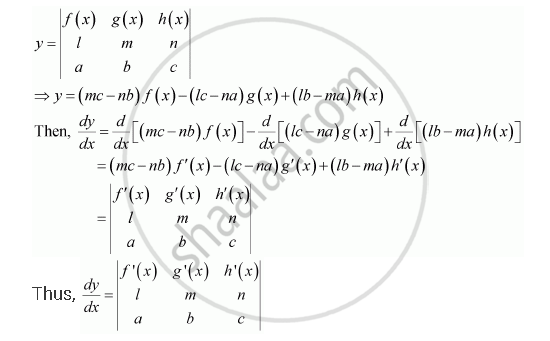
Prove That Dy Dx F X G X H X L M N A B C Mathematics Shaalaa Com

Special Topics In Computational Biology Lecture 4 Enzyme

Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2

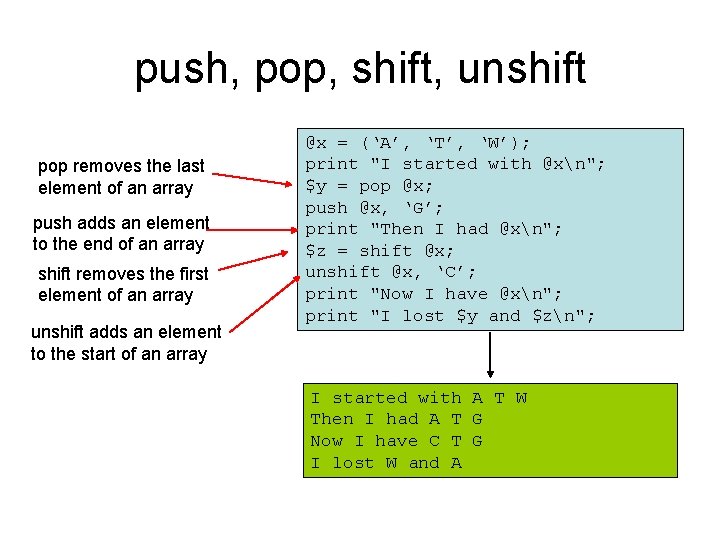
Introduction To Perl For Bioinformatics Thursday April 7

2

Pdf A Formal System Of Axiomatic Set Theory In Coq Semantic Scholar

If Y F X G X H X L M N A B C Prove That Dy Dx F Prime X G Prime X H Prime X L M N A B C

Answered D Y 0 140 If Y X 1 X 2 X Bartleby

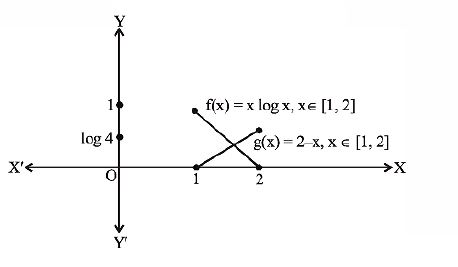
Statement 1 The Equation X Log X 2 X Is Satisfied By At

Midterm Examination With Solutions Advanced Analysis Math 509 Docsity

Vuz Exponenta Ru

In The Graph The Area Above F X Is Shaded And Labeled A The Area Below G X Is Shaded And Labeled Brainly Com

Calculus Cheat Sheet Derivatives Mathematics u0 rhus Studocu

Machine Drawing A Practical Guide To The Standard Methods Of Graphical Representation Of Machines Including Complete Detail Drawings Of A Duplex Pump And Of A Direct Current Generator Section N J Plate E

Direction Write The Letter Of The Correct Answer Gauthmath

Reading Assignment 4

1 If 1 X 0 1 If 0 X 1 Pdf Free Download

Function Definition Types Examples Facts Britannica

The Generalized Van Vleck S Equation On Locally Compact Groups

Corgraculacuanparaa Y D G H V C Vf H X J D H Db D J D G D J X G D J Cb C N C N C B X N V Ch Youtube

Time Series S17 Series 6 Zeitreihenanalyse Mat Studocu

100 In General We Can Define This As If B X A Then X Log B Pdf Free Download

Solved Esttoreraciness And Solve By Finding Integrating Tactar Needed For The Ordinary Differential Equation Ode Zcosh Sinh Sin Solve Problemt1 By Treating tnoull Equation Y Ffx Y G X Y By Making The

2

5 Questions On Electromagnetic Theory I Homework 4 Phy 6346 Docsity

Product Rule Wikipedia

6 Questions Midterm Exam 2 Introduction To Advanced Mathematics Math 215 Docsity

2

If X A B C D And Y F B D G Find I X Y Video

A Diagrammatic Representation Of Motifs Found In The Sequences Of The Download Scientific Diagram

Worldscientific Com

Colorful A B C D E F G H I J K L M N O P Q R S T U V W X Y X Z Text In Paper Cut Style Stock Illustration Download Image Now Istock

Derivative Rules

2

The Geometry Of The Generalized Inverse G Of A Linear Mapping F Here X Download Scientific Diagram

Pdf A Nonlinear Two Dimensional Model

2

Power Series Method And Approximate Linear Differential Equations Of Second Order Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Formule Matematice Active Textbook

L Hopital S Rule Wikipedia

1