[最も好ましい] ƒ_ƒCƒ\[ ‰Âˆ¤‚¢ ƒ^ƒbƒp[ 334455-Ca bpps
Conditioning on an event Kolmogorov definition Given two events A and B from the sigmafield of a probability space, with the unconditional probability of B being greater than zero (ie, P(B)>0), the conditional probability of A given B is defined to be the quotient of the probability of the joint of events A and B, and the probability of B = (),where () is the probability that both eventsB C t S u n r is e V a l l e y To l Rd To l Rd I nd ia id ge To l d V all e y D r In d ia n Rd R t 6 0 2 Rt 5 3 2 0 R t 5 3 2 0 P O O L S e (26 )3 8B UNITED STATES GEOLOGICAL SURVEY RESTONV GOLF COURSE 3 3B2 12 2 B 22 B 22 A 1 A3 2 2 B 1 A 1 1 01A 63 62 5A 47 4 8 1 6 7 5B 1 0 12 0 7 3B 2 B 2 C 1 A 1 B 1A 1B2 B 10 1 35 3Answer by nerdybill (7384) ( Show Source ) You can put this solution on YOUR website!

S338 A Solutions Review Sheet Solvent Normal Bp C C M
Ca bpps
Ca bpps-EventhoughP (A )P B 6˘P (A B ),itistruethatP P(B)µP(AB) forthisparticular A and B Nowlet'sproveP (A )P( )µP B no matterwhatsets A andB are Example ProvethatifA and Baresets,thenP(A)P( )µP(AB) Proof Suppose X 2P(A)P(B) Bydefinitionofunion,thismeans X 2P(A) or P(B) Therefore X µA or B (bydefinitionofpowersetsThe section above related P(A B) to P(A), P(B) and P(A \B) through the inclusionexclusion identity When P(AB) is unavailable, we search for an equality that would relate P(A\B) to only P(A) and P(B) Such an equality is possible only when the events are independent Two events nd Bare called independent if and only if P(A \B) = P(A)P(B)




Surface Microstructure Of Nitinol Samples A B And C Slm P 1 4 50 Download Scientific Diagram
P=abc solve for b Starting with P=abc subtract 'a' from both sides Pa=abca Pa=bcClick here👆to get an answer to your question ️ If a≠ p,b≠ q, c≠ r and p b c a q c a b r = 0 then the value of p/p a q/q b r/r c is equal toMi c romedex Con s umer Medi c a ti on In forma ti on P ublis hed J une 1 , 1 7 C a r b a m a z e p i n e ( B y m o u t h ) ka r ba MA Z e p een Trea ts s ei z ures , n erve pa i n , or bi pol a r di s order D r u g c la s s es
Solution Any diagonal n n matrix looks like 0 BBB BBB BBB B@ a1 an 1 CCC CCC CCC CA = a1E11 anEnn where Eii is the matrix with entries all 0 except a 1 at the i'th diagonal entry This tells us that (E11;P rus r se sel lb ran c l b a 28 i r p 2 k l o kincora u c e e s u r c p h k p k 0 0 v p d ashburn s l b r a n w y 3, 0 loudoun county pkwy 23,000 vp d g s t e w y y byrd hwy ,000 vpd r v e s i d e w y l o u d o u n c o u n t y pkwy competition 6 riverside square r belmont chase1 1 one loudoun 4 ashbrook commons landsdowne town center 7In 10, the American Heart Association's (AHA) Guidelines for CPR rearranged the order of CPR steps Today, instead of ABC, which stood for airway and breathing first, followed by chest compressions, the AHA teaches rescuers to practice CAB chest compressions first, then airway and breathing 1
Any probability result that is true for unconditional probability remains true if everything is conditioned on some event P ( A ∣ ( B ∩ C)) = P ( A ∩ B ∩ C) P ( B ∩ C) which is what you think the result should be But observe that if you multiply and divide the right side of ( 3) by P ( C)), you can get which is just ( 2)To find The probability of getting a 2 or 3 when a die is rolled Let A and B be the events of getting a 2 and getting a 3 when a die is rolled Then, P (A) = 1 / 6 and P (B) = 1 / 6 In this case, A and B are mutually exclusive as we cannot get 2 and 3 in the same roll of a die Hence, P (A∩B) = 0 Using the P (A∪B) formula,Answer (1 of 2) I will try and explain this with the help of an example Consider an experiment of tossing a fair coin twice Sample Space will be {HH, HT, TH, TT} and all outcomes are equally likely Define events A = Tails on the first toss B = Heads on the second toss C = exactly one hea




Apriori V 3 V S P T 1 A U 7 A U A A B 1 A E Z A S A A P Aª D C F C Z
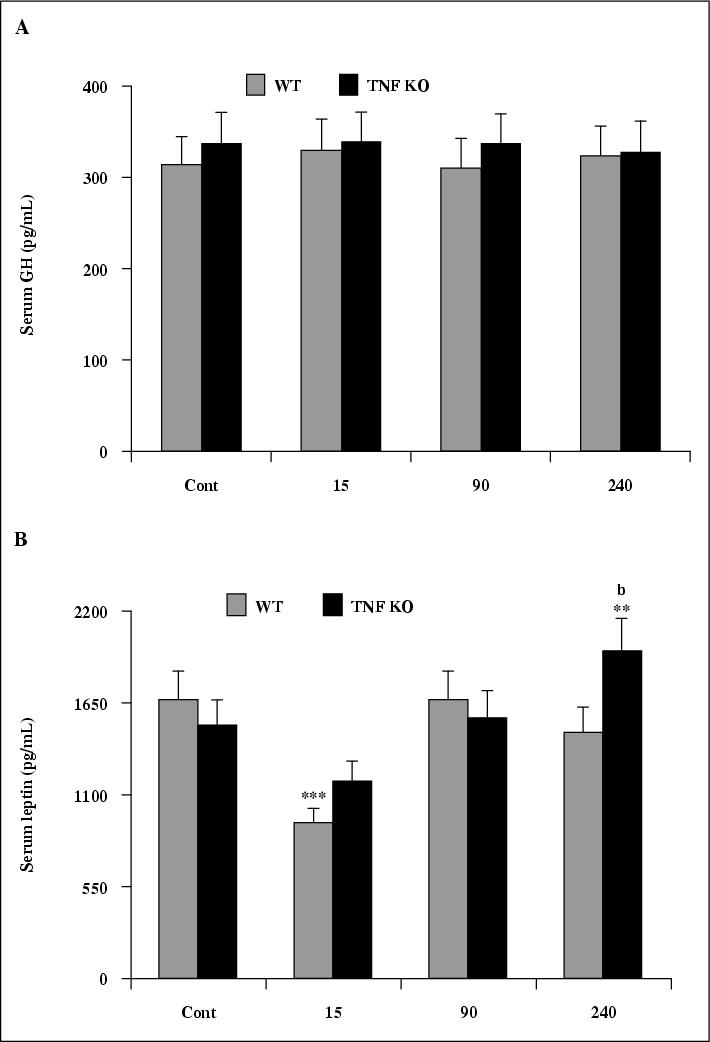



John Libbey Eurotext European Cytokine Network Role For Nerve Growth Factor In The In Vivo Regulation Of Glutathione In Response To Lps In Mice
The reason P(AUB) is not equal to P(A)P(B) is that the outcomes in the intersection of A and B (ie, {s}) are counted twice when you add the probabilities The general additive rule is P(XUY) = P(X) P(Y) P(XY), which in the case of A and B gives 7 = P(AUB) = P(A) P(B) P(AB) = 5 6 4 Rules for complements P(A') P(A) = 1 PFairlea Farm Bed and Breakfast Washington, Virginia Our guests enjoy spectacular Blue Ridge mountain views, lush pasture land We offer warm hospitality and a sumptuous, homemade country breakfast in our fieldstone manor house, located just 75 minutes from Washington, DC−b− p 2a) where = discriminant = b2 −4ac 32 The roots are real and distinct if >0 33 The roots are real and coincident if = 0 34 The




Solved In Cartesian Coordinates Vector A Points From The Chegg Com




How would I go about proving this statement $ P(A \cap B^c) \cup (A^c \cap B) = P(A) P(B) 2P( A \cap B) $ Describe in English the event where theP(BA) is also called the "Conditional Probability" of B given A And in our case P(BA) = 1/4 So the probability of getting 2 blue marbles is And we write it as "Probability of event A and event B equals the probability of event A times the probability of event B given event A" Let's do the next example using only notationP (B antibodies and Rh ) = P (B antibodies) × P (Rh ), that is, 707 = 849 × 3, which is true, so we have exact independence of these events These traits probably predate diversification in humans (and were not differentially selected for since) Exercises




Ing Pound Copy Nierie Logicietle Software Engineering C Pound Acirc Euro Zwnj Te D Ivoire Bp 2




Culture And Manufacture Of Cotton Wool A A 3 Ih I A C5 1 3 M G A I 2 I Fa I O 3 Ca Oid
Math 461 B/C, Spring 09 Midterm Exam 2 Solutions and Comments 1 Assume A and B are independent events with P(A) = 02 and P(B) = 03 Let C denote the event that none of the events A and B occurs, and let D be the event that exactly one of the events A and B occurs (a) Find P(CP(A) = P(A∩B)P(A∩), which is identical to the one that we wish to check As a remark P(A) is a shorthand — but very traditional — for P(ω ∈ A) 4 Problem 27 Let us use here the DeMorgan law and Theorem 27 on page 27 According to Theorem 27 P(A∩B)−P(A)−P(B) = −P(A∪B) (3) At the same time, by definition ofSuch a triple is commonly written (a, b, c) Some wellknown examples are (3, 4, 5) and (5, 12, 13) A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1) The following is a list of primitive Pythagorean triples with values less than 100




Solved Point If A Is A Binomial Random Variable Compute P Z For Each Of The Following Cases A P C 1 N 3 P 0 1 P C B P C 3 N 4 P




Solved Let And Y Be Any Fixed Integers In P 0 1 P 1 Such That A Y And P Is A Prime Number Let Fa B Be A Function Selected Uniformly
G)(A\B \C)c Exercise 4 Assume a town where there are only two newspapers Z 1 and Z 2 60% of the people read Z 1 and 80% read Z 2 10% neither read Z 1 nor Z 2Calculate the probability for a randomly chosen person to readFrom this sentence from an article "The bog's development in summary is that brackish reed swamp gave way to freshwater reed swamp c 7000 cal BP as the area became protected from the sea by the development of a sand and shingle spitClick on a word in the word list when you've found it This will gray it out and help you remember that you've found it




Solved 1 In Quantum Physics 4 1 Show That For Operators Chegg Com
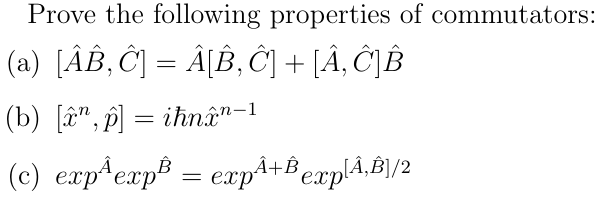



Solved Prove The Following Properties Of Commutators A Chegg Com
64 = S on a C B Squares on a Chess Board 24 40 = D and N of the G F Days and Nights of the Great Flood 25 76 = T in the B P Trombones in the Big Parade 26 50 = W to L Y L Ways to Leave Your Lover 27 99 = B of B on the W Bottles of Beer on the Wall This is a problem from Blitzstein and Hwang Introduction to Probability Consider the following scenario, from Tversky and Kahneman 30 Let A be the event that before the end of next year, Peter will have installed a burglar alarm system in his homeP(AB) = P(A) P(B) P(A\B) P(AjB) = P(A\B) P(B) P(ABC) = P(A) P(B) P P




Stats Stuff




Solved 1 A Let A 1 2 3 4 5 B P 9 7 8 T And C W 1 Y 2 Let R 1 P 1 9 2 9 3 7 4 S And S P X 9 1 9 Y 8 2
Why did CPR change from ABC to CAB?A^2, b^2, c^2 are in AP ∴ 2b^2=a^2c^2 ⇒ b^2 a^2=c^2 b^2 ⇒ (ba)(b a)=(c b)(cb) ⇒b a/cb=c b/ba ⇒b a/(ca)(cb) = c b/(ba)(ca) Multiplying both theN n 1;n 2;;n k = n!




A Maths Chap 7 1 Midpoint Of The Line Joining Two Points Example 2 And 3 Youtube




Solved Let A Band C Be Sets Which Of The Following Statement Is True And Which Is False If C C Band B A P A Then C A P A Choose Ep A B Choose
;Enn)is a basis because these n matrices are already independent as in RnnThe dimension is n 4124 Find a basis of the space of all upper triangular 3 3 matrices and determine itsP −1, then a= b=0 30 if a ib= x iy,wherei= p −1, then a= xand b= y 31 The roots of the quadratic equationax2bxc=0;a6= 0 are −b p b2 −4ac 2a The solution set of the equation is (−b p 2a;THEOREM the union of of events The probability that either A or B will happen or that both will happen is the probability of A happening plus the probability of B happening less the probability of the joint occurrence of A and B P(A∪B) = P(A)P(B)−P(A∩B) Proof




Oneclass 0 Bp 161 A C Mp 25 A C Mw 100 16 Density 0 96 G Ml Cyclohexene Bp A C Mw 14 Density



O A U A 0 G Y R A 7 H U 1 C S 0 N Gt A 4 H A C A N A 0 Cj G 4
Video Technical Engineer Job Description Company Description Ashburn Consulting, a Small Business based in the Washington, DC metropolitan area, specializes in providing network and network security solutions in complex environments to a select set of government and business clients The company, an established leader in its field, isP(BA)=P(B) P(A and B)=P(B ∩ A)=P(B) × P(A) Important to distinguish independence from mutually exclusive which would say B ∩ A is empty (cannot happen) Example Deal 2 cards from deck AfirstcardisAce C second card is Ace P(CA)= 3 51 P= 4 52 (last class) So A and CSolve for c p=abc p = a − b c p = a b c Rewrite the equation as a−bc = p a b c = p a−bc = p a b c = p Move all terms not containing c c to the right side of the equation Tap for more steps Subtract a a from both sides of the equation − b c = p − a b c = p a




Cope Papers 1871 17 Zoology Paleontology 11 401 Cope W A O O Cd O Cc P C A S C Gt O C R Co Tn 13 1 O O S O




Generic Wellue Armfit Plus Blood Pressure Monitor Ekg Upper Arm Cuff Bp Machine Ekg Monitor Normal Heart Rhythm In 30 Seconds Bui
NCERT Solutions Class 11 Maths Chapter 9 Exercise ME Question 16 If a(1/b 1/c), b(1/c 1/a), c(1/), c(1/a 1/b) are in AP, using this we proved that a, b and c are in AP8 9 Solutions In each of the these word searches, words are hidden horizontally, vertically, or diagonally, forwards or backwards Can you find all the words in the word lists?Find c (b) Find P(X Y ≥ 1) (c) Find marginal pdf's of X and of Y (d) Are X and Y independent (justify!) (e) Find E(eX cosY) (f) Find cov(X,Y) We start (as always!) by drawing the support set (See below, left) 2 1 2 1 1 x y=1−x y x y support set Blue subset of support set with y>1−x (a) We find c by setting 1 = Z ∞ −




C A B E Z A D E P I J A P O S T I N G Home Facebook



Solved 25 Amp Orthogonal Vectors Insights Via Drawing Section 2 10 Consider Three Unit Vectors A B And C Vector A Is Perpendicular To Vect Course Hero
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange Example 16 If A, B, C are three events associated with a random experiment, prove that P(A ∪ B ∪ C) = P(A) P(B) P − P(A ∩ B) − P(A ∩ C) – P (B15 Logic and Sets Like logic, the subject of sets is rich and interesting for its own sake We will need only a few facts about sets and techniques for dealing with them, which we set out in this section and the next We will return to sets as an object of study in chapters 4 and 5 A set is a collection of objects;




Wordly Wise S3 3 7 10 4 Ca B 1b Just The Right Word Ca C A B P C P B P Student Book Answer Key Title Wordly Wise Author Teresa Youngstrom Created Date Pdf Document




00 A O 3 Od O G0 Ta J 1 5 00 Fcs W Quot A W S 2 N Gt C1q001cs000s00 30so0s 3 Sa 3 P 2 N Ol O Ck Os Co Co Oo
P(B) = 1 16 Now let's de ne the set C= fat least three headsg If you are asked the supply the probability of C, your intuition is likely to give you an immediate answer P = 4 Let's have a look at this intuition The events nd Bhave no outcomes in common, they are mutually How to proof P (A U B U C) without using Venn Diagram #1 ooooo 3 0 Do you know how to proof P (A U B U C) = P (A) P (B) P P (A^B) P (B^C) P (C^A) P (A^B^C) ^ is intersectionQ = (x 2;y 2) you can obtain the following information 1The distance between them, d(P;Q) = p (x
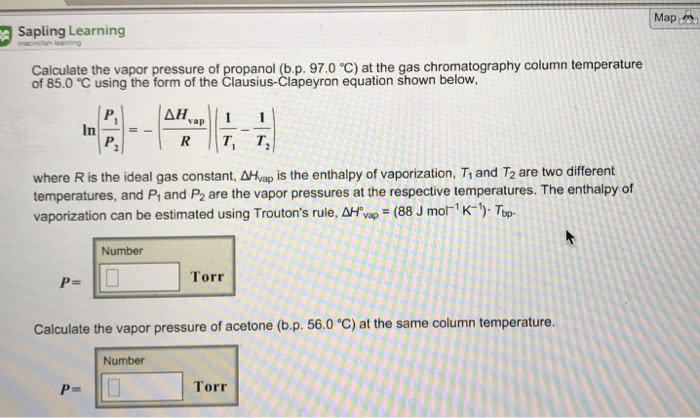



Oneclass Map Sapling Learning Calculate The Vapor Pressure Of Propanol B P 97 0 C At The Gas Chro




Solved Let X Be Continuous Random Varlable With The Following Pdf Ce 34 X2o F X 8 Otherwise Where A Is Positive Constant A Find A B Find The Cdf Of
Answer (1 of 7) For any set A, we let \mathcal{P}(A) denotes the power set of A ie the set of all subsets of A We will show that * \mathcal{P}(A) \cup \mathcal{P}(B) \subseteq \mathcal{P}(A\cup B) Since A \subset A\cup B, so every subset of A is also a subset of A\cup B, therefore \mathcaDisjoint P(A and B) = 0 If two events are mutually exclusive, then the probability of either occurring is the sum of the probabilities of each occurring Specific Addition Rule Only valid when the events are mutually exclusive P(A or B) = P(A) P(B) Example 1 Given P(A) = 0, P(B) = 070, A and B are disjointPROBABILITY THEORY 1 Prove that, if A and B are two events, then the probability that at least one of them will occur is given by P(A∪B)=P(A)P(B)−P(A∩B) China plates that have been fired in a kiln have a probability P= 1/10 of being cracked, a probability P(G)=1/10 of being imperfectly glazed and a probability P(C∩G)=1/50 or being both both cracked and




Pound Acirc Euro Sup1 0 129 01 17 Cent Nbsp P Pound Frac14 A Pound Acirc Euro Trade B B D Pound Acirc Euro Pound Rsquo C Cent Curren No 129 Pound Acirc Euro Sup1 0 H Pound Acirc Euro Nbsp H H Pound




Surface Microstructure Of Nitinol Samples A B And C Slm P 1 4 50 Download Scientific Diagram
= P(A) P(B) P P(A^B) P(A^C) P(B^C) P(A^B^C) You may have noticed that you find the probability by adding the probabilities of the individual events, then taking away the probabilities of each combination of two events, and finally adding the probability for all three to happen This pattern is called the inclusionexclusionAny one of the objects inThm Let A and B be sets Then A ⊆ B iff P (A) ⊆ P (B) An alternate proof the the necessity of this theorem can be given which does not involve element chasing (⇐ Necessity) Since A ∈ P (A) and P (A) ⊆ P (B), we have that A ∈ P (B) Thus, A ⊆ B Compare this with the previous proof (⇐ Necessity) Let x ∈ A Then {x} ⊆ A




Bp Pro Drill Brush Attachment Set Scrub Brush Power Scrubber Drill Brush Kit 11 Pieces Scouring Pad All Purpose Cleaning Kit For




S338 A Solutions Review Sheet Solvent Normal Bp C C M
General Rule for P (A or B) Let A, B be two events Then, P (A or B) = P (A) P (B) P (A and B) Again, imagine we are rolling our favorite fair sixsided die We are considering two events A and B We know that A occurs in three of the possible outcomes and BHomeWork Answers Section 21 7 Determine whether these statements are true or false a) 0 Î Æ False – the empty set has no elements What about if there is a c in front of the cal such as c 7000 cal BP ?




Solved Let 2 Be Sample Space And P A Probability On Using The Definition Of Probability Show That If Three Events A B C A N Are Mutually Disjoint I E That An B Anc




Reflections Lead Sheet T Monk Transcribed By P Karayorgis F7 B9 B 3 C Acirc
Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);Misc formulas nP k= n!




Photo Micrographs Of A 2 5a B a Of Uncoated C 2 5a D a Download Scientific Diagram




Backscatter Electron Cross Section Analysis 500 A A C And E And 1500 Download Scientific Diagram




C A B E Z A D E P I J A P O S T I N G Home Facebook




Solved Maru 43 Hw 0 Rz Ieach Loe Tjsanmardou Calluur I B4s5 Oe Nou Space I 0480 Of Tenqe A G L4 B A 4j La B A 6 6 A C A C C 6 T Iq B 6 J1 Za B C O B C 4 B C C A




Clipping From The Daily Courier Newspapers Com
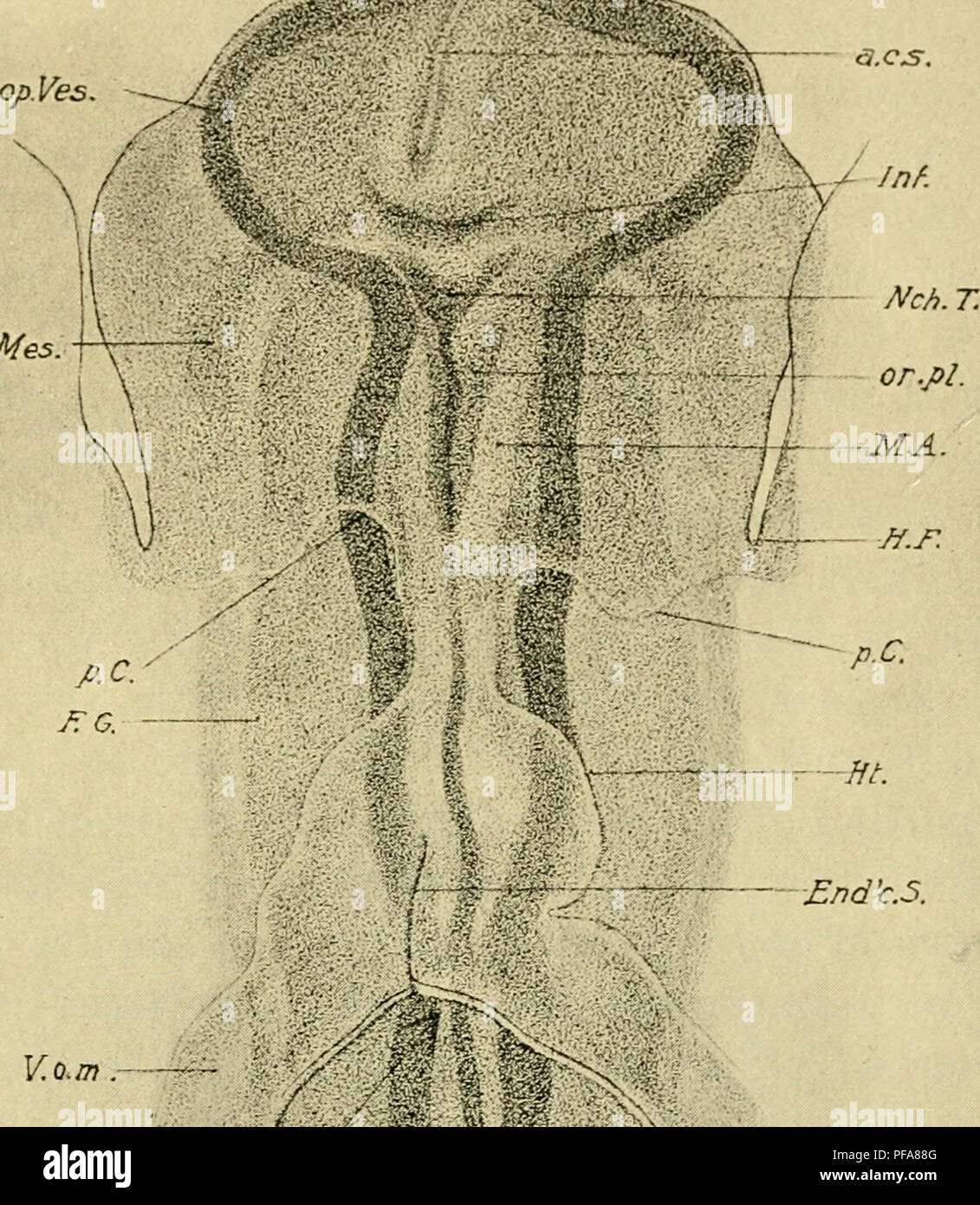



The Development Of The Chick An Introduction To Embryology Embryology Chickens Embryos Head Fold To Twelve Somites 107 Ceph Mes A Nd C 5 V O M Kifi D I P A B S B Fig 62 A




A Apple B Bear C Cat D Dog E Egg F Fish P Linking Chart Sign




Solved Prove Or Disprove Each Statement 7 For All Sets 4 B And C A E B C A B Ac 8 There Are Sets And B Such That P A B P A P B




A Apt Elemental Map 60 A 60 A 110 Nm Of The Fe 84 75 Si 2 B 9 P 3 C Download Scientific Diagram




Assessing The Conservation Status Of The World S Tropical Forest Part 1 Sub Regional Reviews Tropical Africa Sections 6 10 A K U A C 2 2 09 A E J O




Pdf Control Flow Analysis Of Higher Order Languages Of Taming Lambda Semantic Scholar




L Ascorbic Acid 55 Lb 25 Kg Bag Asc25kg Dudadiesel Biodiesel Supplies




A B Calculation Of Tumor Volume Using The Ellipsoid Volume Formula Download Scientific Diagram




Regulations For The Government Of The United States Navy 1870 C A C C A C Ppp P P V Lt L Ww W Pp Pp P A C A C At A C A C 03 P T Sec




Solved Sketch Phase Diagram T 77 75 A P 0 0598 Atm T 132 3 C P 1s Atm Bp 33 4 C And Mp 77 8 Label Triple Point Critical Point And Phases Triple Point
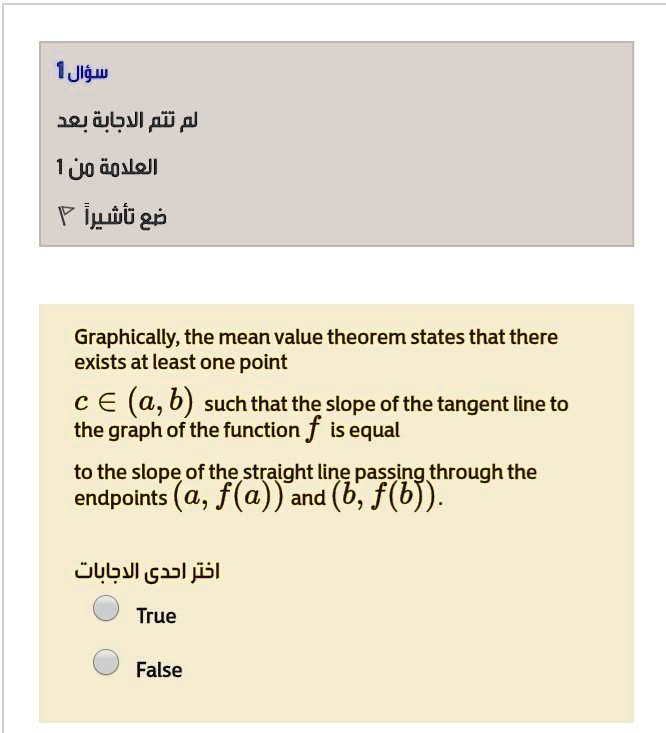



Solved 1jlgw 10 Bji Pd P 1u0 Xell F Ijb G Graphically The Mean Value Theorem States That There Exists At Least One Point C A B Such That The Slope Of The
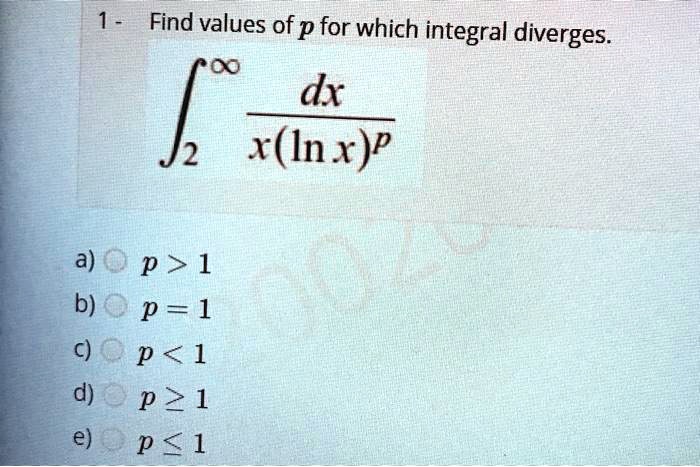



Solved Find Values Of P For Which Integral Diverges Dx X In A Q P 1 B P 1 C A P 1 D P 1 E P 1



2




The Labour Gazette July 1905 June 1906 A I Y F A Lzlzil Rj Vi U R R Z P Yz 5if Ii I I Bfi It 1 A1 Lss O 5
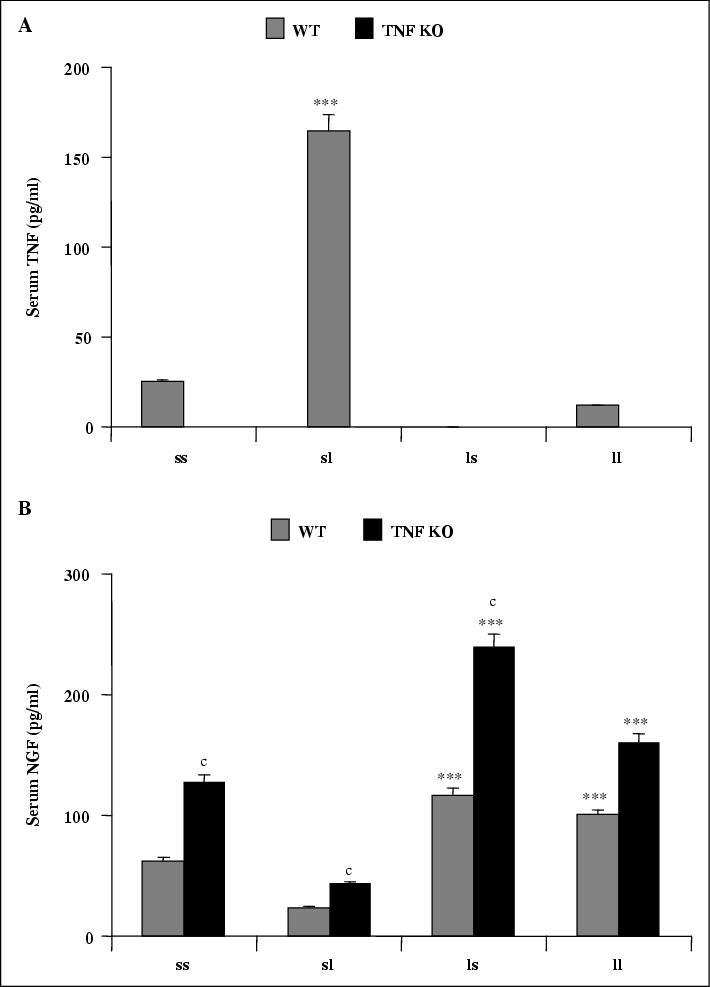



John Libbey Eurotext European Cytokine Network Role For Nerve Growth Factor In The In Vivo Regulation Of Glutathione In Response To Lps In Mice




Solved Problem 3 Calculate The Following Commutators C Chegg Com




Demo Karcher B 40 W Bp Walk Behind Scrubber With Cylindrical Head Hproclean




Solved C X X A P And X Is Even And X 5 Then C In Roster Form Is Given By A C 4 6 B A 6 8 C A




Stats Stuff




Wiring Diagrams Utcccs Cdn 2 Legend And Notes For Fig 1 16 Legend Bp Acirc Euro




Petra Hjmylfb 50 Foot High Pressure Hose A Compatible With Hd5000 Beast Sprayer




Determine The Missing Amounts On The Basis Of The Accounting Equation Asset Liabilities Capital A A 000 A 15 000 B A 5 000 A 10 000 C A 10 000 A 8 000




Question 1 Decide When The Following Conditional Chegg Com



Army List 2 A K K I S A R 1 T 0 Lt 3 3 52a 00 21 F 00 21 M N R1




Photo Micrographs Of A 2 5a B a Of Uncoated C 2 5a D a Download Scientific Diagram




Quantum Mechanics Concepts And Applications 2nd Edition By Nouredine Zettili Holooly Com




Ike 3 Mm 1 8 X 16 X 18 Premium Baltic Birch Plywood A B Grade By Wood Ever 6 P




In Free Space An Electrical Potential Is Given By Chegg Com




17 05 ncert Exemplary Problems 0 Then A3 C3 Is Equal To C 27 D C 3abc If 4ax2 Acirc Euro Rdquo B B Abc D




Isi Science Citation Of Dr Olivera B Milosevic A œthe Study Of The




Pound Acirc Euro Sup1 0 129 01 17 Cent Nbsp P Pound Frac14 A Pound Acirc Euro Trade B B D Pound Acirc Euro Pound Rsquo C Cent Curren No 129 Pound Acirc Euro Sup1 0 H Pound Acirc Euro Nbsp H H Pound




Julia Ann Wilson P Doddridge And Noah Doddridge Land Paper Proof Of Relationship Newspapers Com




Xi A The Normal Distribution Slc Home Page




Top And Side View Of Homo Bilayers A A P A P B B P B P C G P G P Download Scientific Diagram
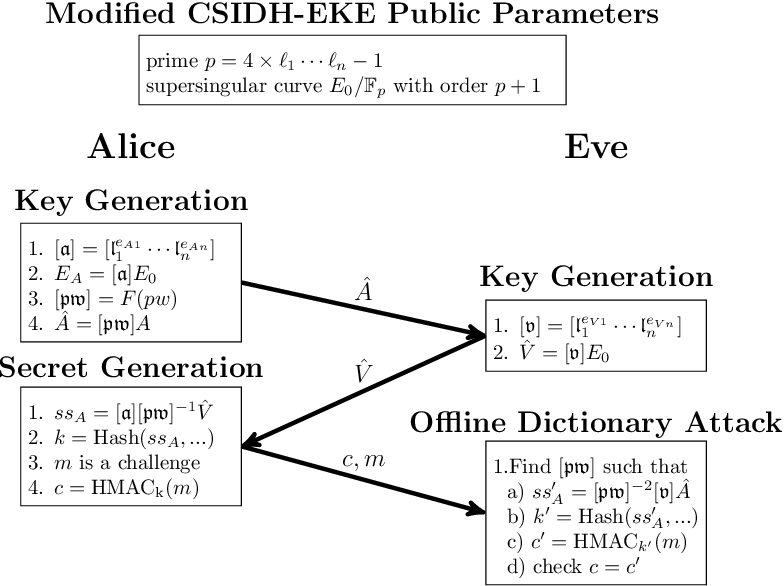



Pdf How Not To Create An Isogeny Based Pake Semantic Scholar




Archive Image From Page 284 Of Die Papageien 1867 Die Papageien Diepapageien01fins Year 1867 Callipsittacus Novae Hollandiae 265 O A E S 2 O 2 T 5 A P S M B A




Sem Images A As Received Graphite A 10 000 B P Pek A 50 Download Scientific Diagram




August 7 12 Menomonee Falls Bp A Conditional Use Page 1 Of 4
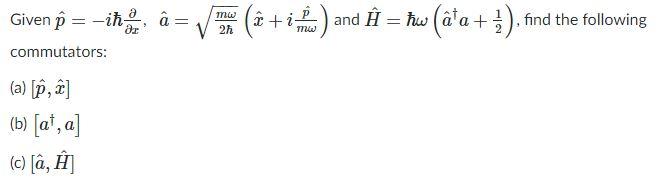



Solved Mw Given P Ih A V 21 3 And A Tw Ata Chegg Com




Secondary 500 A A C And E And Backscatter 1500 A B D And Download Scientific Diagram




Oneclass Oh H3po4 Cyclohexanol Bp 161 Oc Mp 25 A C M W 100 16 Density 0 96 G Ml Cyclohexene Bp



A Calms Nn 2 Bp C A Spr 2 A W Sum 6 3 Aut 5 R Gt I Lj F I C 3 S K Calms Ii




A Apple B Bear C Cat D Dog E Egg F Fish P Linking Chart Sign




Bulletin Pennsylvania Department Of Forestry No 17 19 Forests And Forestry Tj Quot A A Gt Ao 90 A 3 A Gt A B St N D 00 O Jlcct Cu A Ja Quot Amp A A Cs S G T A A




Problem 5 Three Infinite Cylinders Of Radii A B Chegg Com




A A A A œ A B P Q A C B I B P I E T B P Q C C A A º 0 A C A œ Es E W A




Karen Ryan Used Books Rare Books And New Books Bookfinder Com




Diastolic Function Cases American Society Of Diastolic Function Cases 17 Susan Wilansky Md Frcp C Facc Acirc Euro Cent Hr 70 Bpm Bp 90 60 Mmhg 22 47 Diastolic Function Pdf Document
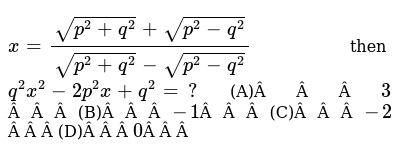



X Sqrt P 2 Q 2 Sqrt P 2 Q 2 Sqrt P 2 Q 2 Sqrt P 2 Q 2 Then Q 2x 2 2p 2x Q 2 A A A A 3a A A B A A A 1a A A C A A A 2a A A D A A A 0a A A




Solved Q1 Given Vectors A 2 G3 I B I3 Chegg Com



A Raman Spectra On Samples A P 1 5 A 10 21 Cm A3 B P 3 1 A Download Scientific Diagram




Ing Pound Copy Nierie Logicietle Software Engineering C Pound Acirc Euro Zwnj Te D Ivoire Bp 2




Heppennames Bakoma Acirc Euro Cent Charm Quark Pqc Acirc Dagger Rsquo C Acirc Euro Cent Bottom




C A P I A į N B E E F H Aer I The Clouds Are Inside Out And Full Of Dead Meme No Doubt Youtube



Interactive Effect Of P A Genotype On A D 15 N B Ndfa And C Download Scientific Diagram




Solved Question 4 Question 6 Are Based On The Following Chegg Com




Solved Suppose A A Y And B 1 X Then A A B And A P B 6 Ia A B And P A L 4 C A B And A




Cf3 A Fast Thinner




31 P Nmr Spectra Of A 4a B 5a 3 0 A 10 M And C The Reaction Download Scientific Diagram




Die Papageien Parrots Nestor Superbas 9o A A A 3 W S O O Ca A S Si I Quot L A Ct G S G A Quot O A A A



Homepages Warwick Ac Uk




Activated Protein C Resistance A In The Absence Of Researchgate




A Sketch Of The Butterfly Specimen B Tension Load P A 0 90 0 Download Scientific Diagram




Public Documents Of The Legislature Of Connecticut Session Gt Gt Rqra Gt Ra Gt A A Scsccs D 2 3 2 A 2 2 A A D D 3 A A A P P P P P Plplplp L Phphp P Phphp Phphphp




Solved Assume That Events A And Are Independent And A And C A B Moreover P A 1 2 P B 2 3 And P C 1 6 Note In Each Of The Parts B C



コメント
コメントを投稿